模型压缩（Model Compression）是指通过一定的算法和策略，在保证模型预测效果满足一定要求的前提下，尽可能地降低模型权重的大小，进而降低模型的推理计算量，内存开销和模型文件的空间占用，最终降低模型推理延迟。因为其可观的收益和一定的预测效果保证，在模型部署和推理之前，通过模型压缩是常使用的技术。

• 常使用的模型压缩技术有：
  • 参数裁剪（Parameter Pruning）和共享（Sharing）
    • 剪枝（Pruning）
    • 量化（Quantization）
    • 编码（Encoding）
  • 低秩分解（Low-Rank Factorization）
  • 知识蒸馏（Knowledge Distillation）
  • …

背景

模型大小持续增长

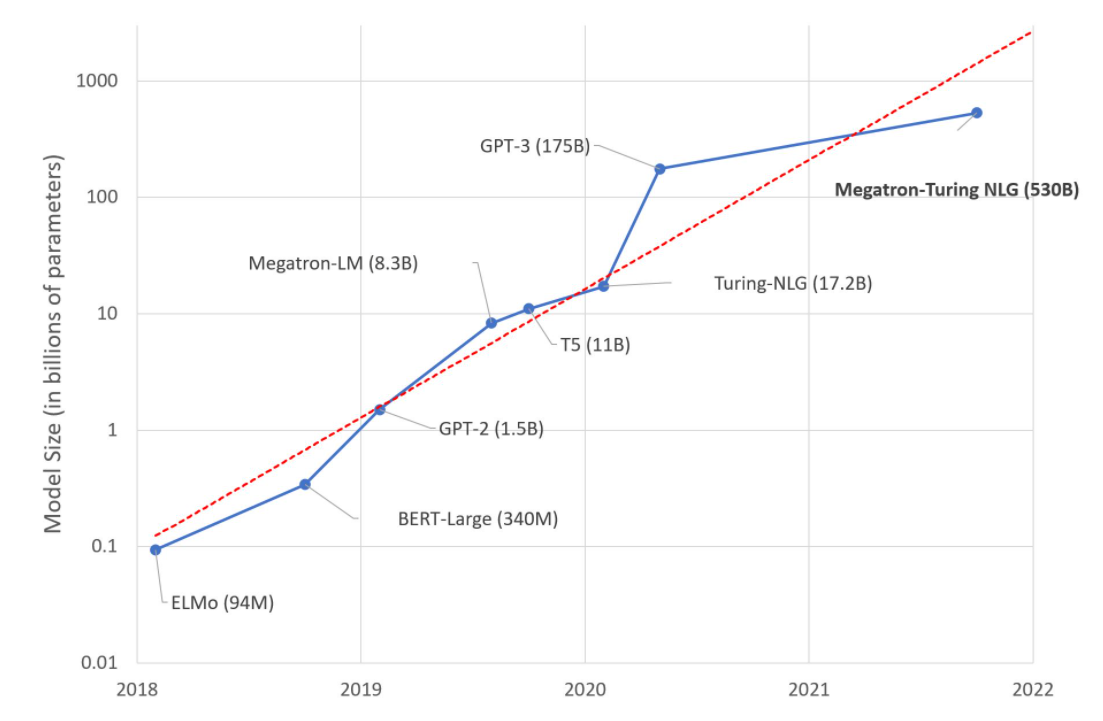
以广泛用于自言语言处理领域的Transformer为例，每年新提出的预训练模型的参数量屡创新高，呈指数型增长。基于 Transformer 的语言模型参数量从 Bert 的亿级，增长到 GPT-2 的十亿级，再到 GPT-3 的千亿级，最大型的语言模型几乎每年增长十倍。 2021年10月，微软公司和英伟达公司宣布了他们共同开发的语言模型 Megatron Turing NLG，该语言模型拥有的模型参数量更是高达5300亿。

训练数据不断增多

大数据促进了大模型的产生，大模型同时也需要大数据作为训练支撑。 全球有数十亿互联网用户，互联网应用层出不穷，互联网每天都在产生、收集和存储大量数据。 未来物联网、电商、短视频和自动驾驶等应用的蓬勃发展，海量数据的来源和多样性会更加丰富。 可以预见的是，未来数据总量将持续快速增长，且增速越来越快。 互联网数据中心 IDC 的数据研究报告指出，全球数据总量从 2012 年的 4 ZB（Zettabyte，十万亿亿字节）增长到了 2018 年的 33 ZB，并预计 2025 年的数据总量将突破175 ZB。 从大数据对模型的需求角度，海量数据需要大模型去拟合。 理论上模型参数越多就能够拟合更多的数据和更复杂的场景。近十年深度学习的发展也一次次的验证，模型越大，效果也好。大力出奇迹，一度成为许多AI算法开发人员的口头禅。 另一方面，从大模型对数据的需求角度，现阶段深度学习模型也必须有大数据的支持。更多的数据量通常可以增强模型的泛化能力，进而带来算法效果的提升。 例如 Imagenet 数据集中图片种类达到了两万多类，图片规模达到了 1400 万张，GPT-3 模型的训练使用了多个数据集中总共约 45 TB 的文本数据。

硬件算力增速放缓

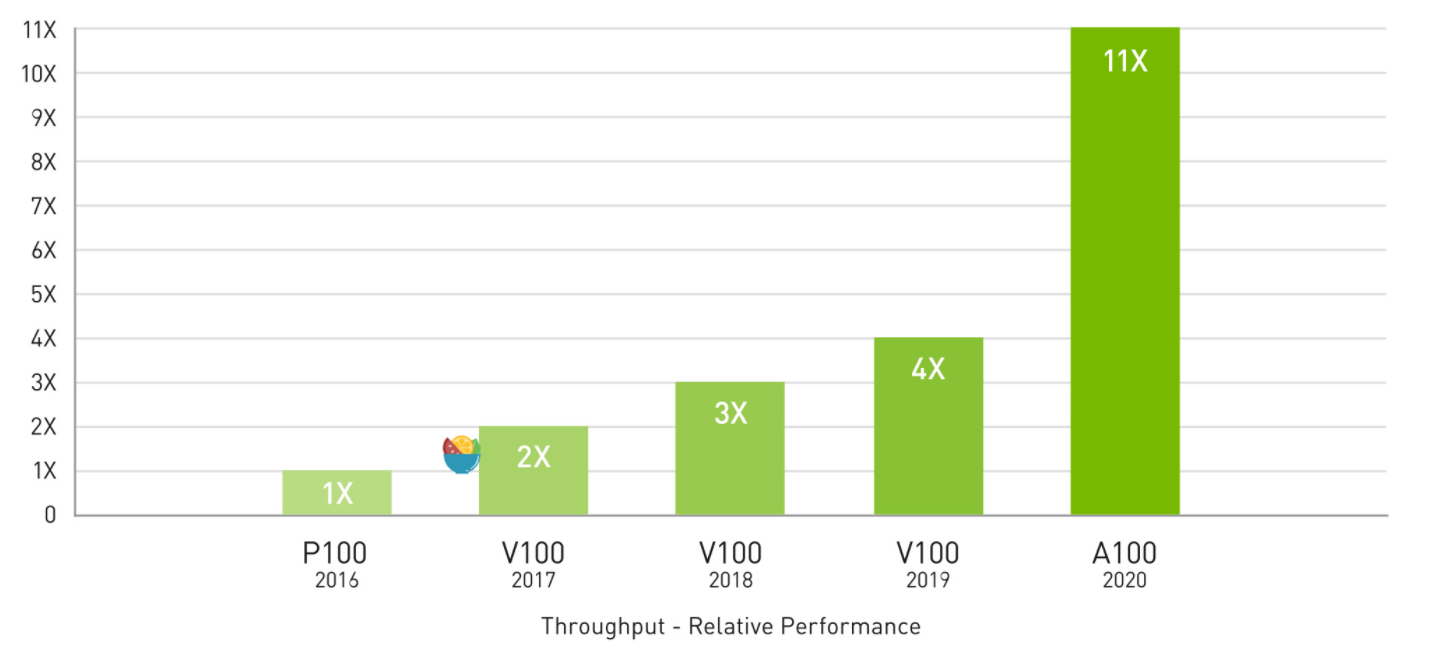
数据、算法和算力是人工智能取得巨大成功的三要素。算力是大数据和大模型的引擎。 近十年以深度学习技术为核心的 AI 热潮就是建立在 GPU 提供了强大的算力基础之上。 如下图所示，英伟达 GPU 的算力近年来一直不断提升，支撑着大模型的不断突破，2020 年的 A100 GPU 相比较于 2016 年的 P100 GPU 性能提升了 11 倍。 2022 年英伟达发布了最新一代的 H100 GPU，相比较于 A100 预计可以带来大约两倍到三倍的性能提升。

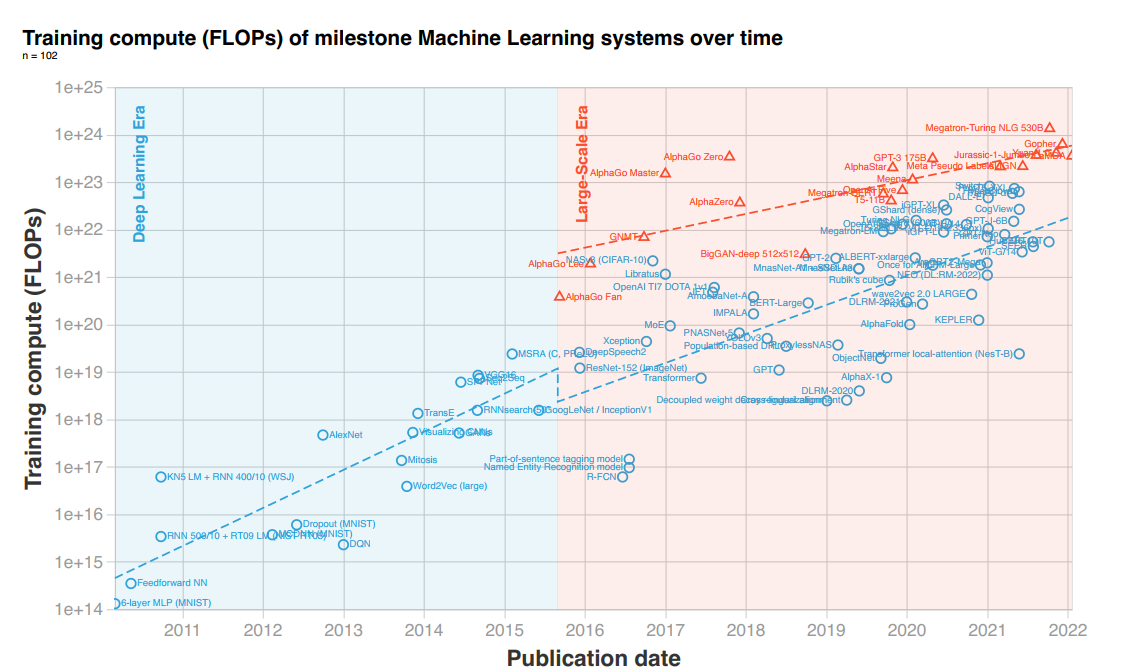
尽管 GPU 硬件性能在英伟达的推动下依然在不断提升，但是如果我们将模型规模增长速度和GPU性能增长速度放在一起比较就会发现，算力的供需之间依然存在巨大差距。 根据相关统计可以发现，2010 年以来深度学习的算力需求增长了 100 亿倍，每 6 个月翻一番，远远超过了摩尔定律每 18 个月翻一番的趋势。

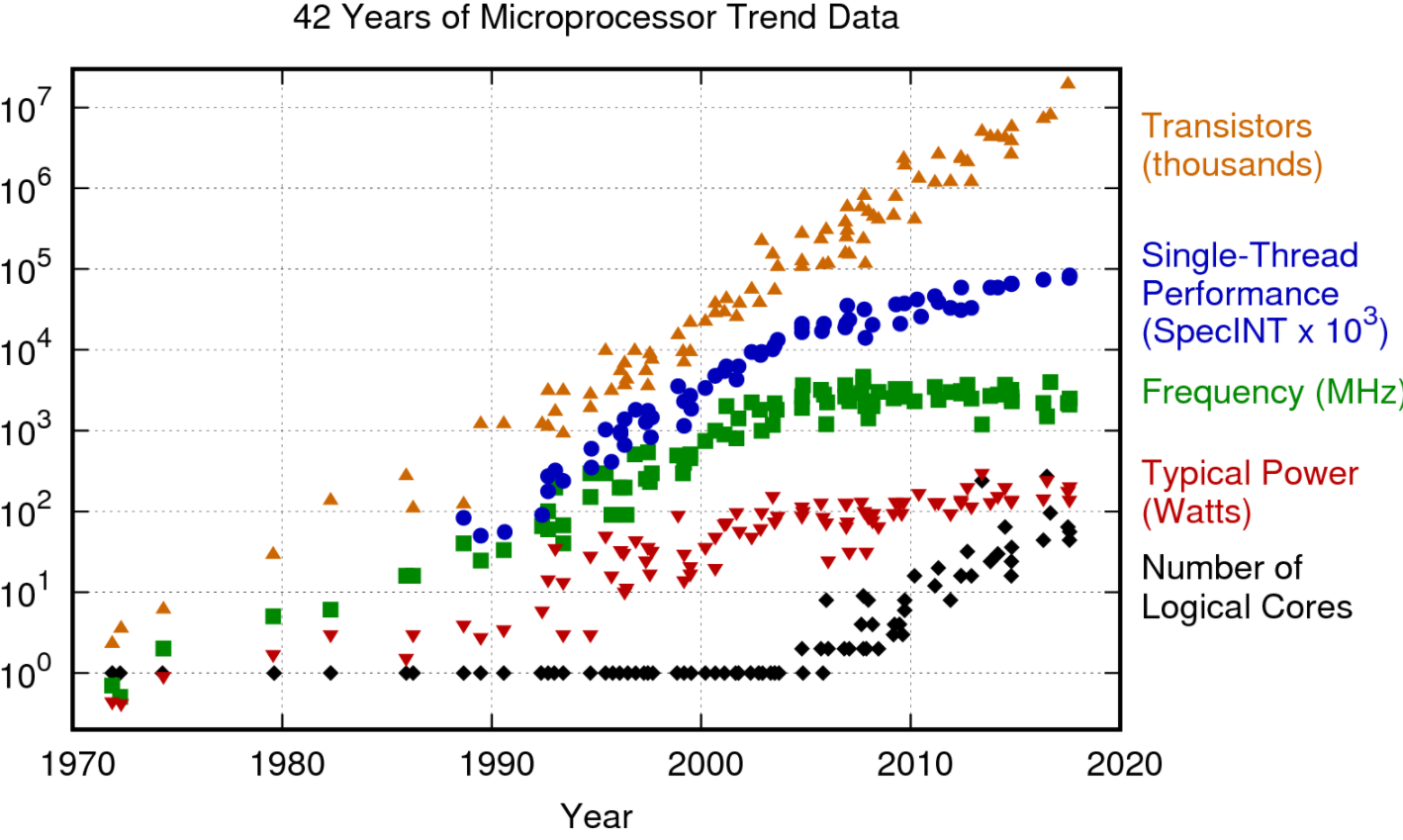
硬件算力的增长同时受到了摩尔定律停滞，登纳德缩放比例定律失效，内存墙等多种因素的制约。 摩尔定律推动了通用处理器性能半个世纪的增长，然而近年来受限于芯片工艺的停滞，通用处理器的频率和晶体管密度都无法持续增长。 通用处理器性能在二十世纪后半叶每年增长约 50% ，验证了摩尔定律的预测，然而近十年来通用处理器性能增速明显放缓，几乎陷于停滞。 经过CPU技术多年的创新与发展，体系结构的优化空间也接近上限，很难再带来显著的性能提升。 通过多核提升处理器性能也受到了功耗的限制。 登纳德缩放比例定律的停滞更是早于摩尔定律，单位面积芯片的功耗不再恒定，更高的晶体管密度意味着更高的功耗。 在传统计算机的冯·诺依曼构架中，存储与计算是分离的。处理器的性能以每年大约 50% 速度快速提升，而内存性能的提升速度则只有每年 10% 左右。 不均衡的发展速度造成了当前内存的存取速度严重滞后于处理器的计算速度，也就是注明的“存储墙”问题。 在大数据和深度学习的人工智能计算时代，更加凸显原本已经存在的“存储墙”问题。 在可预见的将来，算力对模型增长支撑不足的问题会更加严重，算力一定会成为制约 AI 发展和应用的限制因素之一。

数值量化

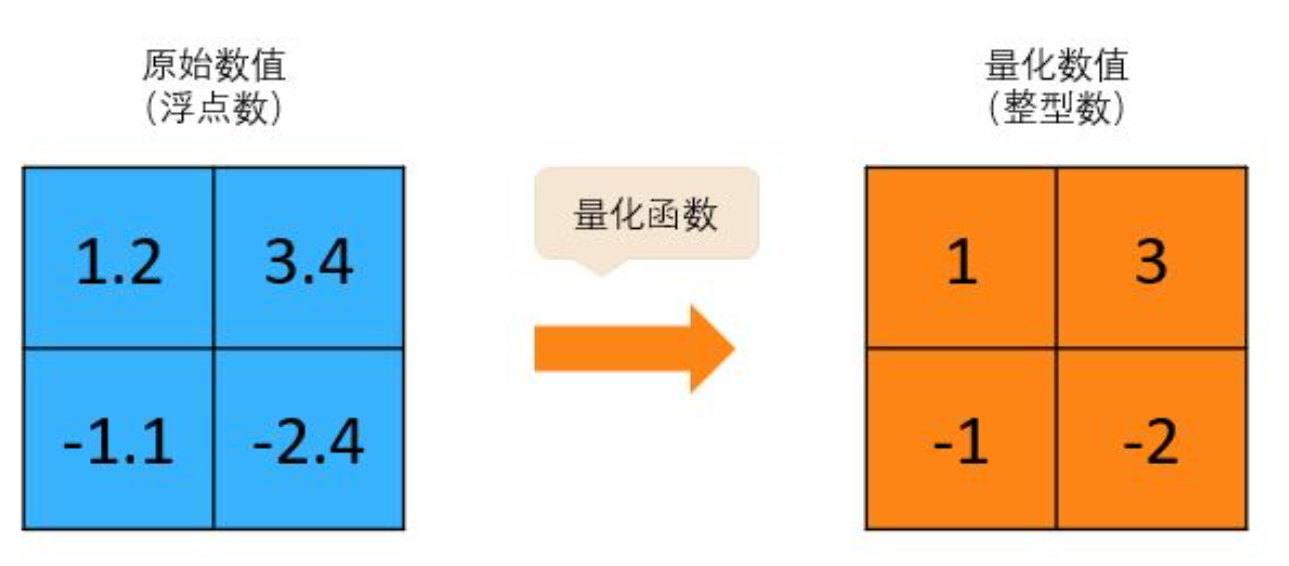
数值量化是一种非常直接的模型压缩方法，例如将浮点数（Floating-point）转换为定点数（Fixed-point）或者整型数（Integer），或者直接减少表示数值的比特数（例如将 FP32 转换为 FP16 ，进一步转化为 Int16 ，甚至是 Int8 ）。 下图是一个非常简单的将浮点数量化为整型数的例子，量化函数可以直接选择 python 中的 int() 函数。

当然实际中的量化函数则更为复杂，需要根据原始权值的分步和目标数值比特数而设计。 数值量化方法根据量化对象可以分为权值量化和激活量化。 权值量化可以直接压缩模型大小，例如将 FP32 压缩成 Int8 可以直接减少四分之三的模型存储需求。 同时对激活进行量化后也可以降低硬件访存和计算开销。 更低的比特位宽通常意味着更快的访存速度和计算速度，以及更低的功耗。 在芯片计算单元的实现中，低比特计算单元也具有更小的芯片面积和更低功耗的优势。

数值量化广泛应用于模型部署场景，原因是模型推理对数值精度并不敏感，没有必要使用浮点数，使用更低比特的定点数或整型数就足以保持模型的准确率。 如何使用更低的比特数以及降低量化对模型准确率的影响是当前研究关注的热点问题之一。 研究和实践表明在大部分应用中使用 8 比特定点进行模型推理足以保证模型准确率。 如果结合一些重训练、权值共享等优化技巧，对于卷积神经网络中的卷积核甚至可以压缩到4比特。 相关甚至尝试只使用三值或二值来表示模型参数，这些方法结合特定硬件可以获得极致的计算性能和效能提升，但受限于数值精度往往会带来模型准确率的损失。

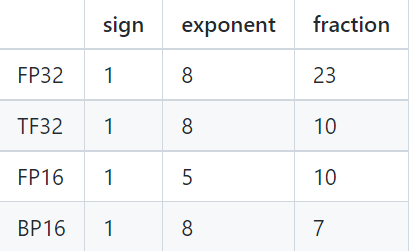
不同于模型推理，模型训练由于需要反向传播和梯度下降，对数值精度敏感性更高，定点数或整型数一般无法满足模型训练要求。低数值精度无法保证模型的收敛性。 因此在模型训练场景中，FP16 ，TF32 ，BF16 等浮点格式则成为了计算效率更高，模型收敛效果更好的选项。常用浮点格式符号位、指数位和尾数位分配如下表。

模型稀疏化

模型的稀疏性是解决模型过参数化对模型进行压缩的另一个维度。 不同于数值量化对每一个数值进行压缩，稀疏化方法则尝试直接“删除”部分数值。 近年来的研究工作发现深度神经网络中存在很多数值为零或者数值接近零的权值，合理的去除这些“贡献”很小的权值，再经过对剩余权值的重训练微调，模型可以保持相同的准确率。

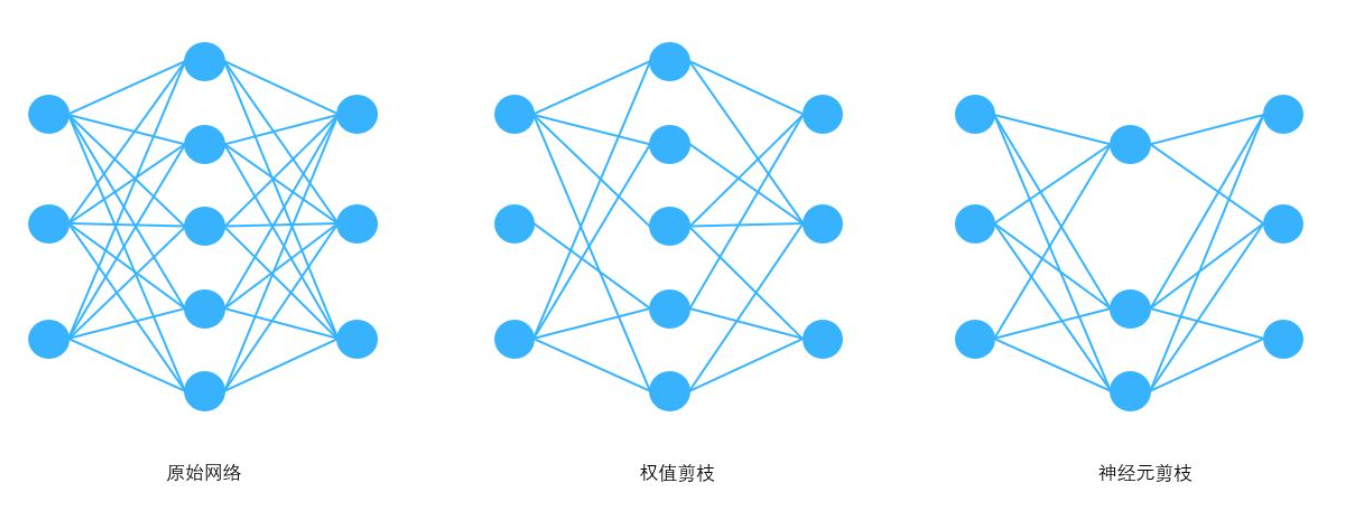
根据稀疏化的对象的不同，稀疏化方法主要可以分为权值剪枝和神经元剪枝。 前者减少神经网络中的连接数量，后者减少神经网络中的节点数量。 当然神经元剪枝后也会将相应的连接剪枝，当某个神经元的所有连接被剪枝后也就相当于神经元剪枝。 对于很多神经网络来说，剪枝能够将模型大小压缩 10 倍以上。

权重稀疏

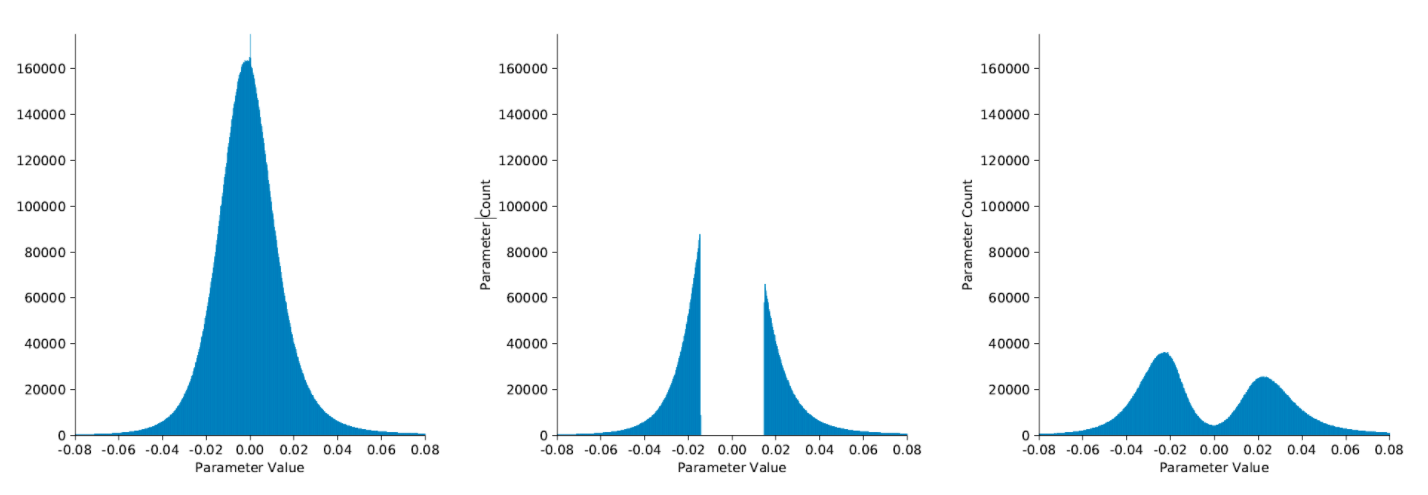
权值剪枝是应用最为广泛的模型稀疏化方法。 在大多数类型的深度神经网络中，通过对各层卷积核元素的数值（即网络权重）进行数值统计，人们发现许多层权重的数值分布很像是正态分布（或者是多正态分布的混合），越接近于0，权重就越多。这就是深度神经网络中的权重稀疏现象，一个典型的网络权重分布直方图如下左图所示。

如果舍弃掉其中接近0值的权重，相当于在网络中剪除部分连接，对网络精度影响并不大，这就是权重剪枝。 这么做的道理是因为权重数值的绝对值大小可以看做重要性的一种度量，较大的权重意味着对最终输出的贡献较大，也相对更加重要，反之则相对不重要。不重要的权重删去对精度影响就应该较小。

即使是移除绝对值接近于0的权重也会带来推理精度的损失。为了恢复网络精度，通常在剪枝之后需要进行再次的训练，这个过程称为微调（fine-tuning）。微调之后的权重分布将部分地恢复高斯分布的特性（如上图右所示），同时网络精度也会达到或接近剪枝前的水平。大多数的权重剪枝算法都遵循这一“正则化-剪枝-微调”反复迭代的流程，直到网络规模和精度的折衷达到预设的目标为止。

然而这种针对每一个权值的细粒度剪枝方法使得权值矩阵变成了没有任何结构化限制的稀疏矩阵，引入了不规则的计算和访存模式，对高并行硬件并不友好。 后续的研究工作通过增加剪枝的粒度使得权值矩阵具有一定的结构性，更加有利于硬件加速。 粗粒度剪枝方法以一组权值为剪枝对象，例如用一组权值的平均值或最大值来代表整个组的重要性，其余的剪枝和重训练方法与细粒度剪枝基本相同。 在CNN中对Channel、Filter 或 Kernel进行剪枝，同样增加了剪枝粒度，也可以认为是粗粒度剪枝。

激活稀疏

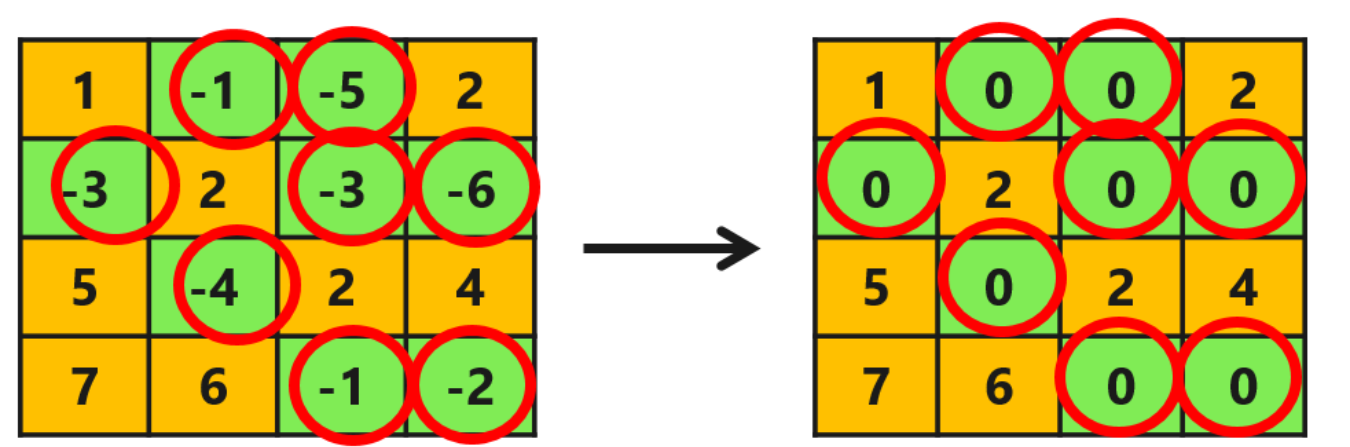
神经网络模型中的非线性激活单元（activation)是对人类神经元细胞中轴突末梢（输出）的一种功能模拟。ReLU激活函数的定义为：

​ \(\phi(x)=max(0,x)\)

该函数使得负半轴的输入都产生0值的输出，特征图经过非线性激活后，产生激活输出，可以看出激活函数给网络带了另一种类型的稀疏性，红圈标识了特征图中被稀疏化的元素。

梯度稀疏

大模型由于参数量庞大，往往需要借助分布式训练的方式在多台节点（Worker）上协作完成。采用分布式随机梯度下降（Distributed SGD）算法可以允许N台节点共同完成梯度更新的后向传播训练任务。其中每台主机均保存一份完整的参数拷贝，并负责其中1/N参数的更新计算任务。按照一定时间间隔，节点在网络上发布自身更新的梯度，并获取其他N−1台节点发布的梯度计算结果，从而更新本地的参数拷贝。

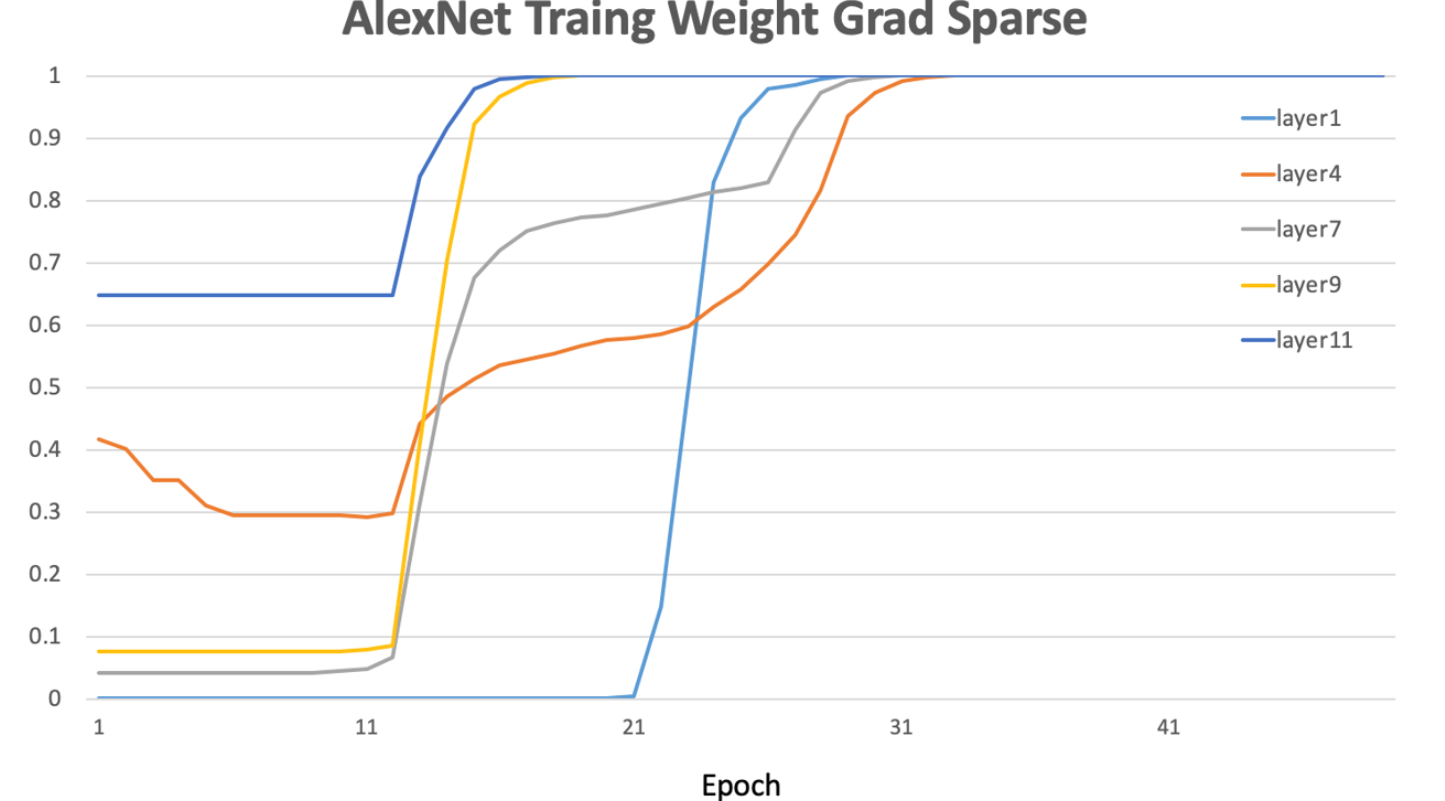
可以看出，随着参与训练任务节点数目的增多，网络上传输的模型梯度数据量也急剧增加，网络通信所占据的资源开销将逐渐超过梯度计算本身所消耗的资源，从而严重影响大规模分布式训练的效率。另一方面，大多数深度网络模型参数的梯度是高度稀疏的，研究表明在分布式SGD算法中，99.9%的梯度交换都是冗余的。下图AlexNet的训练早期，各层参数梯度的幅值还是较高的。但随着训练周期的增加，参数梯度的稀疏度显著增大，大约30个训练周期后，各层梯度稀疏度都趋于饱和。显然，将这些0值附近的梯度进行交换，对网络带宽资源是一种极大的浪费。

梯度稀疏的目的在于压缩分布式训练时被传输的梯度数据，减少通信资源开销。由于SGD算法产生的梯度数值是高度噪声的，移除其中并不重要的部分并不会显著影响网络收敛过程，与之相反，有时还会带来正则化的效果，从而提升网络精度。梯度稀疏实现的途径包括：

1）预设阈值：在网络上仅仅传输那些幅度超过预设阈值的梯度；

2）预设比例：在网络上传输根据一定比例选出的一部分正、负梯度更新值；

3）梯度丢弃：在各层梯度完成归一化后，按照预设阈值丢弃掉绝大多数幅值较低的梯度。

一些梯度稀疏算法在机器翻译任务中可以节省99%的梯度交换，而仅带来0.3%的模型精度损失；可以将ResNet-50模型训练的梯度交换参数量从97MB压缩为0.35MB而并不损失训练精度。