算子
目前已支持yolo5,resnet等模型的推理
实现要点
- 快速:利用硬件的加速特性,好的算法,并行计算
- 准确:跟训练框架的计算结果对齐
- 融合不同路线:
TFLite,NCNN通过手写实现算子,TVM通过编译和规则配置来自动实现算子
下面介绍其中几个算子的实现。
Relu
使用OpenMP进行多线程计算,一个线程计算一个batch的数据。 使用SSE指令集进行SIMD计算,同时对4个单精度浮点数做计算。替换成AVX指令集后,运行时间可以降低40%。
InferStatus ReluLayer::Forward(const std::vector<std::shared_ptr<Tensor<float>>>& inputs,
std::vector<std::shared_ptr<Tensor<float>>>& outputs) {
...
#pragma omp parallel for num_threads(batch_size)
for (uint32_t i = 0; i < batch_size; ++i) {
const std::shared_ptr<Tensor<float>>& input = inputs.at(i);
std::shared_ptr<Tensor<float>> output = outputs.at(i);
float* in_ptr = const_cast<float*>(input->raw_ptr());
float* out_ptr = const_cast<float*>(output->raw_ptr());
// delcare vector of type __m128 with all elements set to zero
__m256 _zero = _mm256_setzero_ps();
const uint32_t size = output->size();
// 256(bit) / 32(bit/float) = 8 float number
const uint32_t packet_size = 8;
uint32_t j = 0;
for (j = 0; j < size - 3; j += packet_size) {
// Load 256-bits from memory into dst. mem_addr must be aligned on a 32-byte boundary
__m256 _p = _mm256_load_ps(in_ptr);
__m256 _value = _mm256_max_ps(_zero, _p);
_mm256_store_ps(out_ptr, _value);
in_ptr += packet_size;
out_ptr += packet_size;
}
if (j < size) {
while (j < size) {
float value = input->index(j);
output->index(j) = value > 0.f ? value : 0.f;
j += 1;
}
}
}
return InferStatus::kInferSuccess;
}
卷积
使用im2col方法,也就是把卷积计算的过程转换成矩阵运算的过程。优点是只需要进行一次矩阵乘法运算,大大减少了内存的访问次数。同时矩阵乘法运算优化比较成熟,效率较高。
-
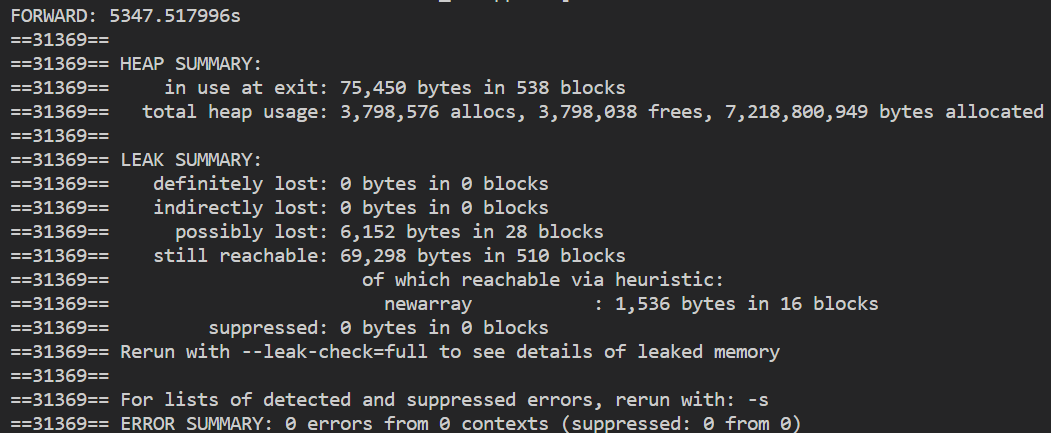
首先需要将卷积核、输入特征图进行展开。先考虑单通道输入特征图,单个单通道卷积核的情况。下图红色的是输入特征图,灰色的是卷积核。
-
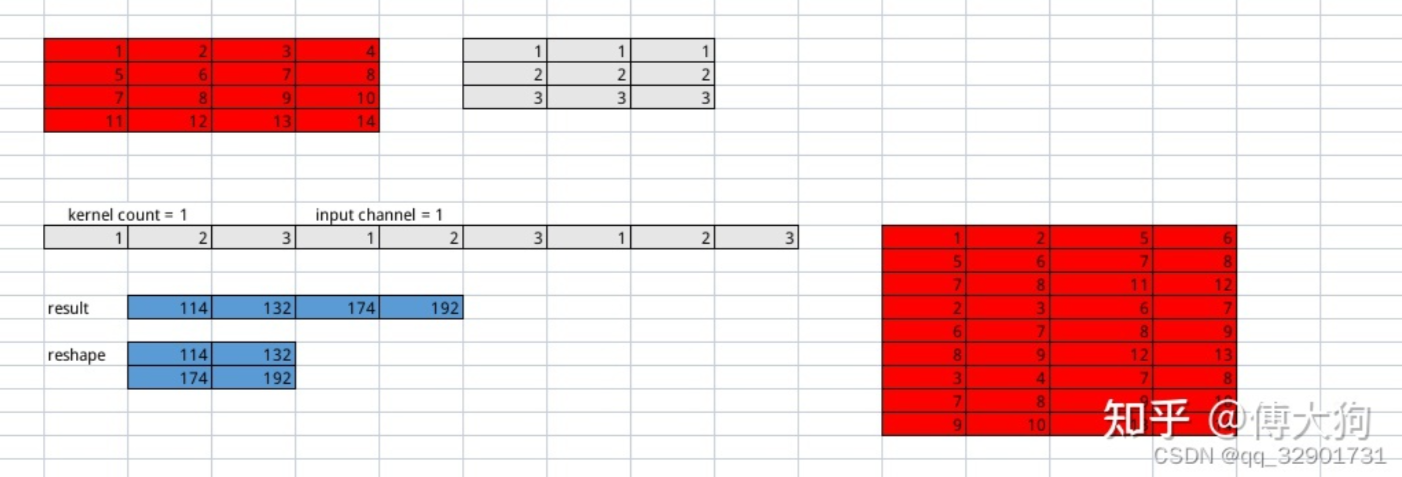
再考虑多通道输入特征图,单个多通道卷积核的情况,不同颜色表示不同的输入通道。

-
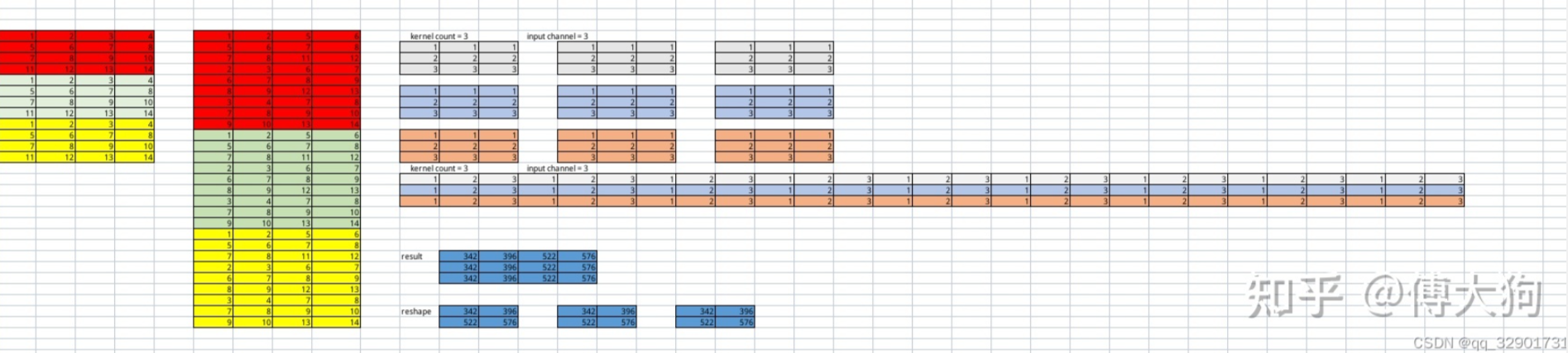
最后考虑多通道输入特征图,多个多通道的卷积核的情况,即有多个输出通道。
/**
* 初始化kernel的im2col排布
*/
void ConvolutionLayer::InitIm2ColWeight() {
......
const uint32_t kernel_count_group = kernel_count;
std::vector<arma::frowvec> kernel_matrix_arr(kernel_count_group);
arma::frowvec kernel_matrix_c(row_len * kernel_c);
for (uint32_t k = 0; k < kernel_count_group; ++k) {
const std::shared_ptr<Tensor<float>>& kernel = this->weights_.at(k);
for (uint32_t ic = 0; ic < kernel->channels(); ++ic) {
memcpy(kernel_matrix_c.memptr() + row_len * ic,
kernel->slice(ic).memptr(), row_len * sizeof(float));
}
kernel_matrix_arr.at(k) = kernel_matrix_c;
}
this->kernel_matrix_arr_ = std::move(kernel_matrix_arr);
......
}
/**
* 初始化输入特征图的im2col排布
*/
arma::fmat ConvolutionLayer::Im2Col(sftensor input, uint32_t kernel_w, uint32_t kernel_h,
uint32_t input_w, uint32_t input_h, uint32_t input_c_group,
uint32_t group, uint32_t row_len, uint32_t col_len) const {
// img2Col之后的输入特征图
arma::fmat input_matrix(input_c_group * row_len, col_len);
for (uint32_t ic = 0; ic < input_c_group; ++ic) {
const arma::fmat& input_channel = input->slice(ic + group * input_c_group);
int current_col = 0;
for (uint32_t w = 0; w < input_w - kernel_w + 1; w += stride_w_) {
for (uint32_t r = 0; r < input_h - kernel_h + 1; r += stride_h_) {
float* input_matrix_c_ptr = input_matrix.colptr(current_col) + ic * row_len;
current_col += 1;
for (uint32_t kw = 0; kw < kernel_w; ++kw) {
const float* region_ptr = input_channel.colptr(w + kw) + r;
memcpy(input_matrix_c_ptr, region_ptr, kernel_h * sizeof(float));
input_matrix_c_ptr += kernel_h;
}
}
}
}
return input_matrix;
}
矩阵乘法底层调用OpenBlas的实现。此外还实现了分组卷积。
表达式(Expression)
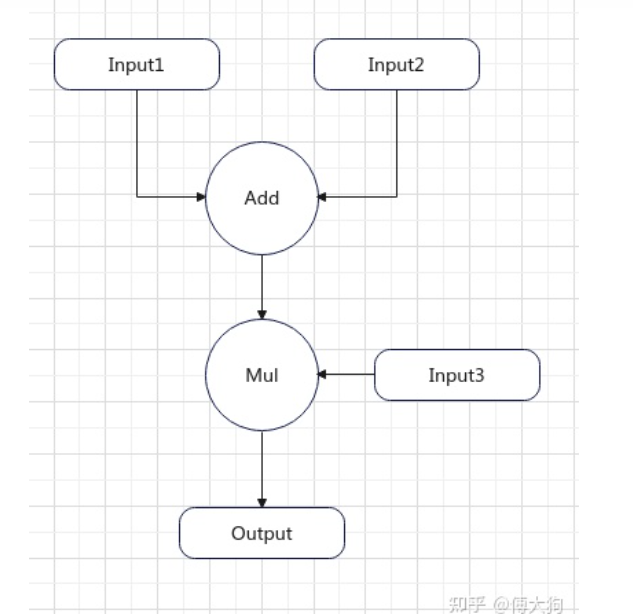
表达式就是一个计算过程,类似于如下:
output_mid = input1 + input2
output = output_mid * input3
-
如下图所示:
PNNX的Expession Operator中给出的是一种抽象表达式,表达式会对计算过程进行折叠,消除中间变量. 并且将具体的输入张量替换为抽象输入@0,@1等.对于上面的计算过程,PNNX生成的抽象表达式是这样的:
add(@0,mul(@1,@2))
这就需要提供鲁棒地表达式解析和语法树构建功能,具体过程分为词法解析、语法解析及表达式计算。
词法解析
词法解析的目的就是将add(@0,mul(@1,@2))拆分为多个token,token的设计如下:
enum class TokenType {
TokenUnknown = -1,
TokenInputNumber = 0,
TokenComma = 1,
TokenAdd = 2,
TokenMul = 3,
TokenLeftBracket = 4,
TokenRightBracket = 5,
};
struct Token {
TokenType token_type = TokenType::TokenUnknown;
int32_t start_pos = 0; //词语开始的位置
int32_t end_pos = 0; // 词语结束的位置
Token(TokenType token_type, int32_t start_pos, int32_t end_pos): token_type(token_type), start_pos(start_pos), end_pos(end_pos) {
}
};
最终得到的token依次为add ( @0 , mul等。
语法解析
当得到token数组之后,对语法进行分析,得到抽象语法树。树节点定义如下:
struct TokenNode {
int32_t num_index = -1;
std::shared_ptr<TokenNode> left = nullptr;
std::shared_ptr<TokenNode> right = nullptr;
TokenNode(int32_t num_index, std::shared_ptr<TokenNode> left, std::shared_ptr<TokenNode> right);
TokenNode() = default;
};
语法解析的过程是递归向下的,定义在Generate_函数中。如果当前token类型是输入数字类型, 则直接返回一个操作数token作为一个叶子节点,不再向下递归。
if (current_token.token_type == TokenType::TokenInputNumber) {
uint32_t start_pos = current_token.start_pos + 1;
uint32_t end_pos = current_token.end_pos;
CHECK(end_pos > start_pos);
CHECK(end_pos <= this->statement_.length());
const std::string &str_number =
std::string(this->statement_.begin() + start_pos, this->statement_.begin() + end_pos);
return std::make_shared<TokenNode>(std::stoi(str_number), nullptr, nullptr);
}
如果当前Token类型是mul或者add. 那么我们需要向下递归构建对应的左子节点和右子节点。
else if (current_token.token_type == TokenType::TokenMul || current_token.token_type == TokenType::TokenAdd) {
std::shared_ptr<TokenNode> current_node = std::make_shared<TokenNode>();
current_node->num_index = -int(current_token.token_type);
index += 1;
CHECK(index < this->tokens_.size());
// 判断add之后是否有( left bracket
CHECK(this->tokens_.at(index).token_type == TokenType::TokenLeftBracket);
index += 1;
CHECK(index < this->tokens_.size());
const auto left_token = this->tokens_.at(index);
// 判断当前需要处理的left token是不是合法类型
if (left_token.token_type == TokenType::TokenInputNumber
|| left_token.token_type == TokenType::TokenAdd || left_token.token_type == TokenType::TokenMul) {
// (之后进行向下递归得到@0
current_node->left = Generate_(index);
} else {
LOG(FATAL) << "Unknown token type: " << int(left_token.token_type);
}
}
-
最终生成如下的抽象语法树:
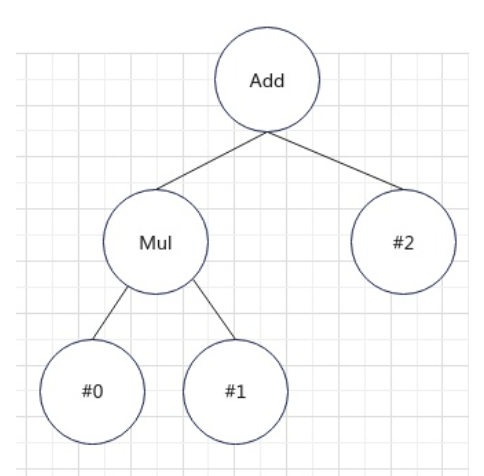
表达式计算
将抽象语法树后序遍历得到逆波兰表达式(后缀表达式),即操作数在前,算子在后的形式
@0,@1,mul,@2,add
依次遍历逆波兰表达式,如果遇到操作数,则压入栈中;如果遇到操作符,先弹出栈内的两个操作数,再进行计算。
性能测试
Benchmark
-
可以发现batch=8、16的时候,CPU运行时间低于总时间,CPU没有打满,batch=4就好很多。
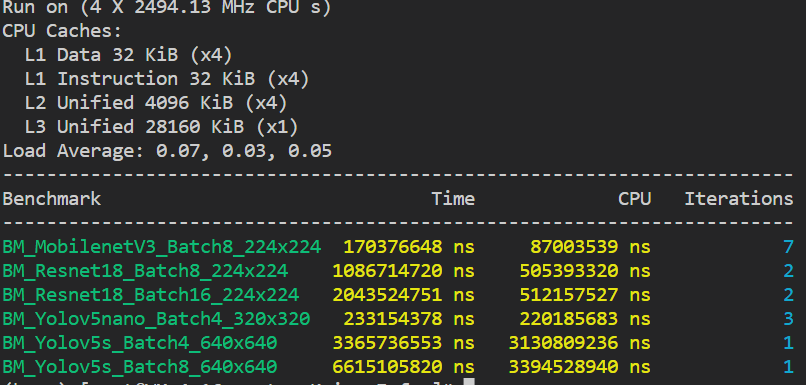
Yolov5s耗时分析
-
卷积计算最耗时

-
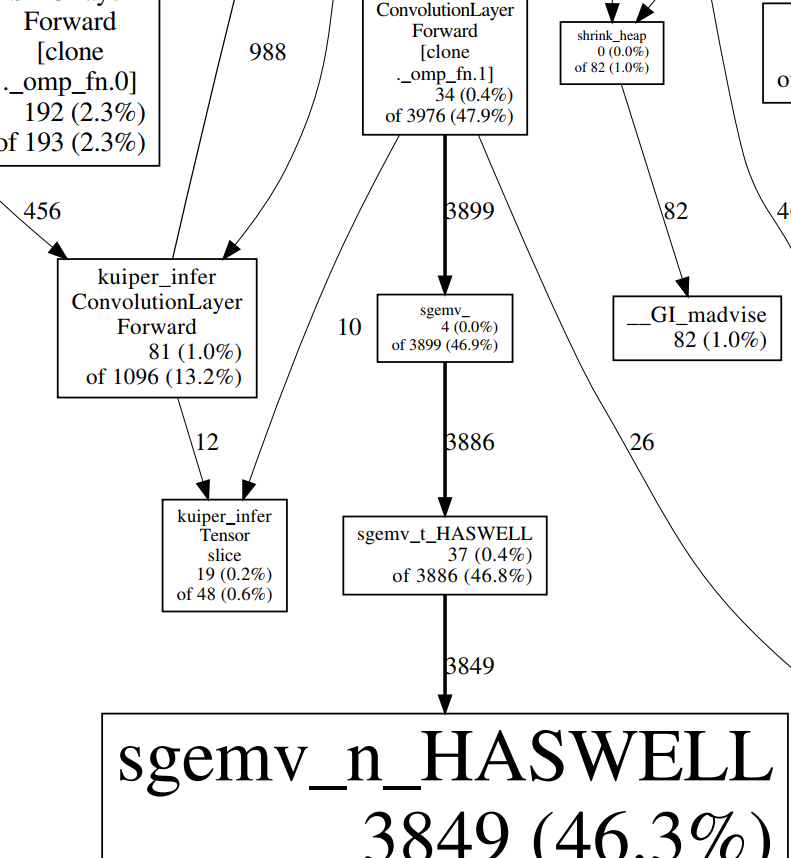
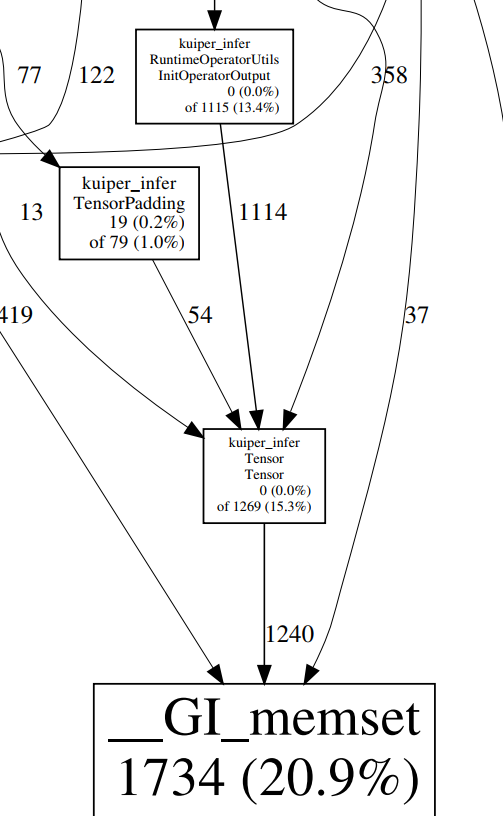
gperftool显示执行时间最长的函数是sgemv,耗时占46.3%,sgemv函数执行矩阵-向量运算。排第二的是memset,其执行的是复制字符的操作。

-
通过graph call可以发现sgemv主要是卷积层在调用
-
memset函数主要是InitOperatorOutput在调用
内存泄漏检测
其它
- 图像前处理&后处理:
opencv - 日志:
glog - 单元测试:
google test
参考资料
-
https://github.com/zjhellofss/KuiperInfer
-
https://zhuanlan.zhihu.com/p/593215728