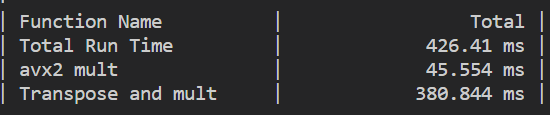气象预报、石油勘探、核子物理等现代科学技术大多依赖计算机的计算模拟,模拟计算的核心是表示状态转移的通用矩阵乘(GEMM)。此外,通用矩阵乘也是深度学习中的主要的算子实现算法,例如,卷积,全连接,平均池化,注意力等算子均可以转换为 GEMM。
GPU 和其他专有人工智能芯片 ASIC也针对矩阵乘的计算特点提供底层硬件计算单元的支持(例如 NVIDIA GPU 张量核(Tensor Core),Google TPU 脉动阵列的矩阵乘单元(Matrix Multiply Unit)等)。
二维矩阵 A(M x K )和二维矩阵 B(K x N)相乘,生成矩阵C(M x N)
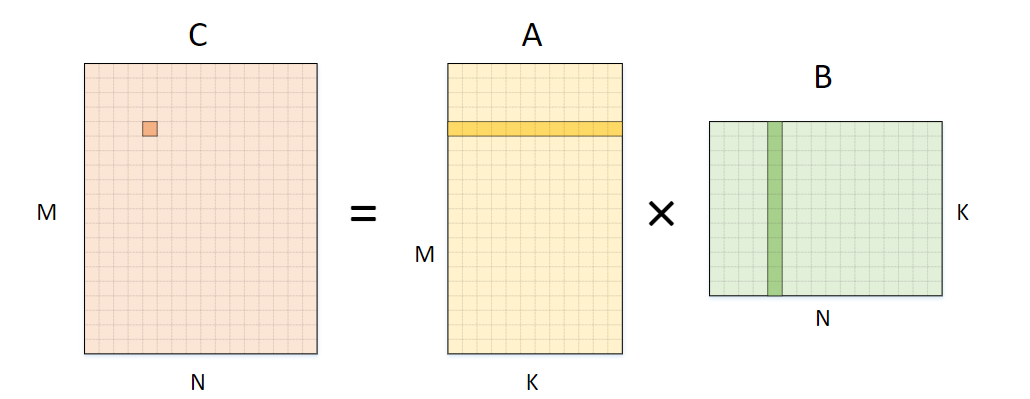
naive的实现如下:
// 遍历矩阵A的行
for (uint64_t i = 0; i < M; i++){
// 遍历矩阵B的列
for (uint64_t j = 0; j < N; j++) {
float accum = 0; // 避免false sharing
// 逐元素相乘再加和
for (uint64_t k = 0; k < K; k++){
accum += A[i*K+k]*B[k*N+j];
}
C[i*N+j] = accum;
}
}
除了二维矩阵相乘,通常会遇到矩阵A是高维的情况。例如三维矩阵 A(L x M x K)和二维矩阵 B(K x N)相乘,生成矩阵C(L x M x N),可以把三维矩阵的前两维看做一个整体,转换成二维矩阵相乘,实现如下:
for (uint64_t i = 0; i < LM; i++){
// 遍历矩阵B的列
for (uint64_t j = 0; j < N; j++) {
float accum = 0;
for (uint64_t k = 0; k < K; k++){
accum += A[i*K+k]*B[k*N+j];
}
C[i*N+j] = accum;
}
}
GEMM的算法优化可分为两类:
- 基于算法分析的方法:根据矩阵乘计算特性,从数学角度优化,典型的算法包括Strassen 算法和 Coppersmith–Winograd 算法。
- 基于软件优化的方法:根据计算机存储系统的层次结构特性,选择性地调整计算顺序,主要有循环拆分向量化、内存重排等。
下面将简要介绍几种典型的方法。
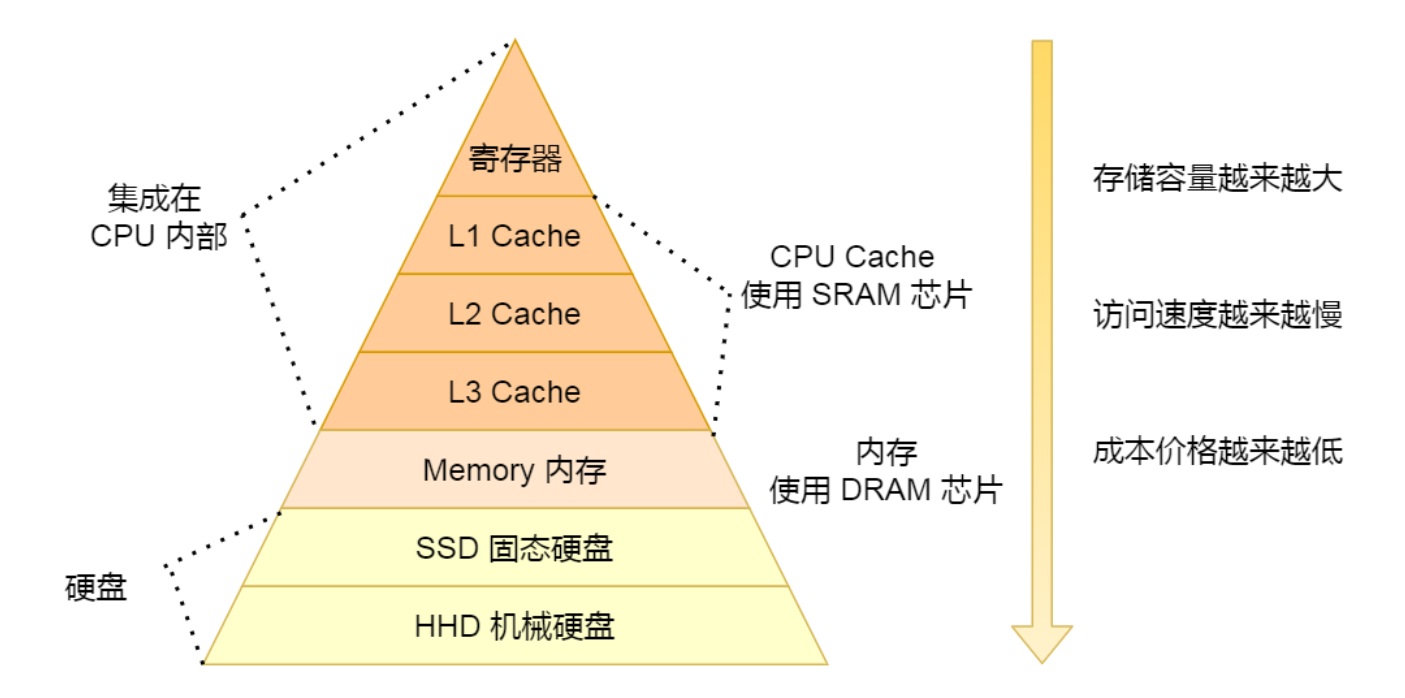
缓存
当代计算机的CPU计算速度比内存的读取速度要快得多(即von neumann bottleneck),为了减少内存访问对性能的影响,一个方法是引入缓存。为了更好地利用缓存,有如下的优化方法:
分块(tiling)
把矩阵分块,直到缓存可以容纳分块后的矩阵。例如2个128B*128B*128B的矩阵乘法运算,只需要访问一次内存,就可以在大小为512KB的缓存中完成。
空间访问局部性
Cache line(缓存行)是计算机处理器中的缓存中的基本单位,它是一块固定大小的内存块,通常是 64 字节。当处理器需要访问一个内存地址时,它会首先检查缓存中是否存在该内存地址的缓存行。
如果缓存中已经存在该缓存行,则处理器可以直接从缓存中读取数据,这比从内存中读取数据要快得多。如果缓存中不存在该缓存行,则处理器需要从内存中读取整个缓存行,并将其存储到缓存中。
M*L的矩阵A和L*N的矩阵B进行矩阵乘法,naive的过程如下:
for (uint64_t i = 0; i < M; i++){
for (uint64_t j = 0; j < N; j++) {
float accum = 0;
for (uint64_t k = 0; k < L; k++){
accum += A[i*L+k]*B[k*N+j];
}
C[i*N+j] = accum;
}
}
存在一个问题:对于矩阵B,第k次访问的是位置是(k,j),第k+1次访问的是位置是(k+1,j)(如下左图),也就是每次访问都是跨行的。因为元素是按行主序存放在内存中的,下一个访问的元素跟之前访问的元素间隔太远,很有可能不在一个Cache line里面,因此需要重新访问内存,这样降低了效率。
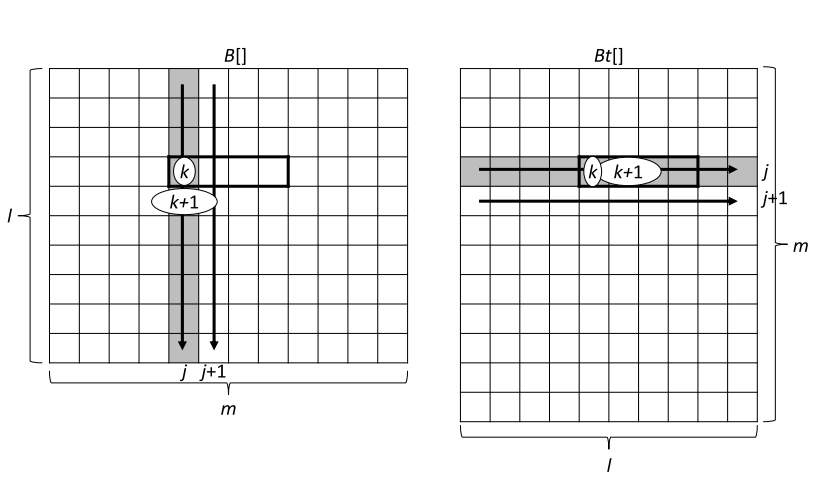
为了解决这个问题,可以把矩阵B进行转置,计算过程如下,这样对矩阵B每次访问的元素都是相邻的(如上图右)。
for (uint64_t k = 0; k < L; k++)
for (uint64_t j = 0; j < N; j++)
Bt[j*L+k] = B[k*N+j];
for (uint64_t i = 0; i < M; i++){
for (uint64_t j = 0; j < N; j++) {
float accum = 0;
for (uint64_t k = 0; k < L; k++)
accum += A[i*L+k]*Bt[j*L+k];
C[i*N+j] = accum;
}
}
多线程/OpenMP
#pragma omp parallel for collapse(2)
for (uint64_t i = 0; i < M; i++){
for (uint64_t j = 0; j < N; j++) {
for (uint64_t k = 0; k < L; k++)
C[i*N+j] += A[i*L+k]*Bt[j*L+k];
}
}
Avoid False Sharing
多核场景下,每个核都一个自己的L1-cache(如下图)。多线程程序如果要同时修改在同一个Cache line里面的数据,会导致其它核的cache数据失效,其它核也需要重新从主存读取数据,这就叫做false sharing。
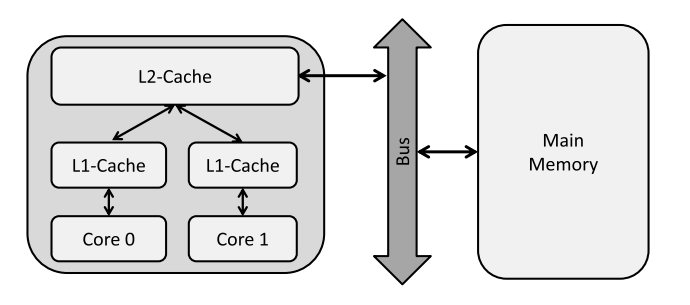
避免false sharing的方法,就是不要频繁修改cache line里面的数据,尽量使用中间变量来存储中间结果。
#pragma omp parallel for collapse(2)
for (uint64_t i = 0; i < M; i++){
for (uint64_t j = 0; j < N; j++) {
float accum = 0;
for (uint64_t k = 0; k < L; k++)
accum += A[i*L+k]*Bt[j*L+k];
C[i*N+j] = accum;
}
}
SIMD
#pragma omp parallel for collapse(2)
for (uint64_t i = 0; i <M; ++i){
for (uint64_t j = 0; j < N; ++j){
__m256 X = _mm256_setzero_ps();
for (uint64_t k = 0; k < L; k+=8){
const __m256 AV = _mm256_load_ps(A+i*L+k);
const __m256 BV = _mm256_load_ps(B+j*L+k);
X = _mm256_fmadd_ps(AV,BV,X);
}
C[i*N+j] = hsum_avx(X);
}
}
性能提升
可以看到,最原始的实现耗时22.5s,编译器03优化之后为3.85s,avx2的实现耗时45ms,提升了500倍!